Probability is the branch of mathematics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an event is to occur. Probability Mathematics Grade 12 Notes and Study Guides free download
PROBABILITY GRADE 12 NOTES – MATHEMATICS STUDY GUIDES
8.1 Revision
Probability is the study of how likely it is that an event will happen. The following questions are typical probability questions:
- What is the chance that it will rain tomorrow?
- If I buy a Lotto ticket, what is the chance that I will win the Lotto?
We can use a probability scale to decide what chance there is of an event happening.

|
8.2 Theoretical probability and relative frequency
If you flip a coin:
- The possible outcomes are H (heads) or T (tails).
- There are two possible outcomes. Each has a 50% chance of happening.
- We say that there is a theoretical probability of ½ for each outcome.

The theoretical probability of getting the outcome heads (H), is written as P(H).
P(H) = ½
Relative frequency
Try this experiment:
• Flip a coin 10 times. Did it land on heads exactly 5 out of 10 times?
e.g.1
- Mantse flipped a coin 10 times and it landed on heads 7 times. So for her experiment, the relative frequency of heads is 7/10.
- Jake flips a coin 100 times and records his results. His record shows that he flipped heads 55 times. So the relative frequency of heads is 55/100 . Therefore, the relative frequency of tails is 45/100.
- Jake flips the coin 1 000 times. Now it is likely that heads and tails will come up about the same number of times. He is likely to get heads 499 to 501 times.
Now the relative frequency is equal to or close to the theoretical probability of ½
Relative frequency is called Empirical probability or Experimental probability
Although the theoretical probability of getting heads is ½, your experiment often does not show this exactly. The results of your experiment give you the relative frequency of getting heads in that particular experiment.
|

8.3 Venn diagrams
We use Venn diagrams to help us to represent different events. Venn
Diagram consists of circles and a rectangle
The rectangle S represents the sample space (all of the possible outcomes).
Each circle inside S represents a different event.
If the two circles intersect, the intersection shows which outcomes belong to both events.

e.g.2
Draw a Venn diagram to show the sample space
S = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10}
Indicate the following events in the sample space:
Event A is the set of prime numbers.
∴A = {2; 3; 5; 7}
Event B is the set of even numbers.
∴ B = {2; 4; 6; 8; 10}

|
e.g.3
Use the Venn diagram in the previous example to determine:
- P(A)
- P(B)
- P(A and B)
- P(A or B)
Solutions
|
- P(A)+P(B) – P(A and B)
= 4/10 + 5/10 – 1/10 = 8/10 = 4/5 - P(A or B) = 8/10 = 4/5
∴ P(A or B) = P(A)+P(B) – P(A and B)
8.4 Mutually exclusive events
Mutually exclusive events are events that cannot happen at the same time.
There is no intersection between the events.
- Mutual: applies to two or more people or events.
- Exclude: to keep out, not allow a person in.
- Mutually exclusive: Both events keep the other out. So there is no outcome that can happen in both events at the same time.
e.g.4
If you roll a die, it is impossible for it to land on a 1 and a 6 at the same time. So P(1) and P(6) are mutually exclusive.
When you roll a die, what are the chances of getting a 6 or a 1?
So P(1 or 6) = P(1) + P(6) = 1/6 + 1/6 = 2/6 = 1/3
So the chance of rolling either a 1 or a 6 is 1/3 or 33,3%
S: Possible outcomes for rolling a die

When two events are mutually exclusive, P(A and B) = 0
∴ P(A or B) = P(A) + P(B) for mutually exclusive events
We can also use this rule for the number of elements or outcomes in each event, if the events are mutually exclusive:
n(A or B) = n(A) + n(B)
When the two events are mutually exclusive, then they do not overlap.
Therefore the intersection of A and B is empty and we write A∩B = ∅ (empty set) and P(A∪B) = 0
If P(A and B) = 0 or if P(A or B) = P(A) + P(B), then the events are mutually exclusive
8.5 Complementary events
Events that are mutually exclusive and make up the whole sample space are called complementary events. There is no intersection and no elements from the sample set are outside the two sets.
The possible events when you roll a die are 1; 2; 3; 4; 5 or 6.
The probability of rolling a 4 is 1/6.
The probability of not rolling a 4 is 5/6 .
So the event not rolling a 4 is the complement of the event rolling a 4.
So P(4) + P(4´) = 1/6 + 5/6 = 1
The complementary rule:
P(A´) + P(A) = 1 or P(A´) = 1 – P(A)
P(A´) means probability of ‘not A’.

In the example, n(not rolling a 4) + n(rolling a 4) = 5 + 1 = 6
Activity 1
- If S = {1; 2; 3; 4; 5; 6; 7}, A = {1; 3; 5; 7} and B = {2; 4; 6}, what is the probability of choosing a number that is not in set A? (2)
- S = {a; b; c; d; e; f; g; h; i; j} and A = {a; e; i}, B = {b; c; d; f; g; h}, C = {b; h; j}.
- Draw a Venn diagram to represent S. (4)
- Give a description of set A. (1)
- Are there any complementary sets? Explain. (2)
- Which sets are mutually exclusive, but they are not complementary? Give a reason for your answer. (2)
- A DVD shop has 180 comedies, 250 drama films, 230 science fiction movies and 120 thrillers. If you select a DVD at random, what is the probability that this movie is a comedy OR a thriller? (3)
[14]
- Complement: (noun) something that completes an event; it adds what is missing to make up the whole.
- Complementary: (adjective) an event that completes or adds to other events to make up the whole sample space.
NOTE: A complement is not the same as a compliment!
A compliment is a positive comment made to a person or a group of people.
Solutions
|
8.6 Events which are not mutually exclusive
Sometimes two events have some outcomes that are the same.
e.g.5
The sample space S = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}
In the sample space, event A is the set of multiples of 3.
So Set A = {3; 6; 9; 12}
Event B is the set of odd numbers.
So B = {1; 3; 5; 7; 9; 11}
P(A) = favourable outcomes = 4 = 1
possible outcomes
P(B) = 6 = 1
12 2
So P(A) + P(B) = 4 + 6 =10
12 12 12
P(A or B) is the chance of getting the numbers in set A or in set B.
We cannot count the 3 and the 9 for both sets. We cannot repeat the numbers in the intersection of set A and set B.
So P(A or B) = 8
12
So P(A) + P(B) ≠ P(A or B)
To make them equal, we need to subtract the probability of the intersection, P(A ∩ B)
P(A) + P(B) – P(A ∩ B) = 4 + 6 – 2 = 8 This is the answer we found for P(A or B).
12 12 12 12
The ADDITION rule for the probability of ANY two events in a sample space:
P(A or B) = P(A) + P(B) – P(A ∩ B)
We can also use this rule for the number of elements or outcomes in each set:
n(A or B) = n(A) + n(B) – n(A ∩ B)
Activity 2
In a group of 50 learners, 35 take Mathematics and 30 take History.
12 learners do not take Mathematics or History.
- Draw a Venn diagram to represent this information. (4)
- If a learner is chosen at random from this group, what is the probability that he takes both Mathematics and History? (2)
[6]
Solutions
|
8.7 Summary of symbols and sets used in probability
There are some symbols you need to use when describing probability. We have used some of them already.
To explain the use of each symbol, we will use these sets again:
S = {a; b; c; d; e; f; g; h; i} and A = {a; e; i}, B = {a; b; c; d; f; g;}, where S= Sample Space, A and B are two sets is the sample space
P(A) – (A) means the probability that an element from set A will occur.
P(A) = 3/9 = 1/9
n(A) – n(A) means the number of elements in set A.
n(A) = 3
A´ – A´ means all the elements of the sample space that are NOT in set A. This is the complement of set A.
A´ – = {b; c; d; f; g; h}
∪ – A ∪ B means the same as A OR B.
It means the union of the two sets and represents the total of all the elements that are in set A or set B. No elements are repeated.
A ∪ B = {a; b; c; d; e; f; g; i}
∩ – A ∩ B is the same as A and B.
It means the intersection of sets A and B and represents all the elements that they share. (All the elements that are in both set A and set B at the same time). This is where the sets overlap.
A ∩ B = {a}
P(A ∩ B) – P(A ∩ B) means the probability that an element from (A ∩ B) will occur. P(A ∩ B) = 1/9
P(A ∪ B) – P(A ∪ B) means the probability that an element from (A ∪ B) will occur. P(A ∪ B) = 8/9
n(A ∪ B) – n(A ∪ B) means the number of elements in set A or set B.
n(A ∪ B) = 8
n(A ∩ B) n(A ∩ B) means the number of elements in set A and set B at the same time (the elements they share). n(A ∩ B) = 1
(A ∩ B)´ (A ∩ B)´ means all the elements of the sample space that are NOT in (A ∩ B), the complement of A ∩ B.
(A ∩ B)´ = {b; c; d; e; f; g; h; i}
(A ∪ B)´ (A ∪ B)´ means all the elements of the sample space that are NOT in (A ∪ B).
(A B)´ = {h}
 You also need to be able to work with three sets in probability, using a Venn diagram and the formulae.
You also need to be able to work with three sets in probability, using a Venn diagram and the formulae.

The shaded areas represent:
(A or B or C) or (A ∪ B ∪ C)

e.g.6
A survey is conducted with a group of 50 learners to find out what is more popular at the school tuckshop. They are asked if they usually buy toasted sandwiches (T), salads (S) or burgers (B).
They can choose none, one, two or three of the meals.
The survey results are shown with this Venn diagram:

- How many people did not buy salads, toasted sandwiches or burgers?
- Calculate the probability that a learner selected at random from this survey:
- buys salad, but not toasted sandwiches or burgers.
- buys toasted sandwiches and salad, but not burgers.
- buys salad or burgers or both, but not toasted sandwiches.
Solutions:
|
Activity 3
A school organised a camp for 103 Grade 12 learners. The learners were asked which food they prefer for the camp.
They had to choose from chicken (C), vegetables (V) and fish (F).
The following information was collected:
- 2 learners do not eat chicken, fish or vegetables
- 5 learners eat only vegetables
- 2 learners only eat chicken
- 21 learners do not eat fish
- 3 learners eat only fish
- 66 learners eat chicken and fish
- 75 learners eat vegetables and fish
Let the number of learners who eat chicken, vegetables and fish be x.
- Draw a Venn diagram to represent the information. (6)
- Calculate x. (3)
- Calculate the probability that a learner, chosen at random:
- Eats only chicken and fish, and no vegetables. (2)
- Eats any TWO of the given food choices: chicken, vegetables and fish. (2)
[13]
Solutions:
|
8.8 Tree diagrams and contingency tables
- Independent events
Two successive events are independent if the outcomes of the one event do not influence the outcomes of the other event.e.g.7
The probability of flipping a coin and it lands on heads is P(H) = ½ .
What is the probability of flipping two coins and they both land on heads?Solution
There are four possible outcomes:
H and H; H and T; T and H; T and T.
So H and H is 1 out of 4 outcomes and P(H and H) = ¼ .A tree diagram is a picture that helps you to list all possible outcomes of the events.
Here is the tree diagram for P(H and H) if you flip a coin twice:
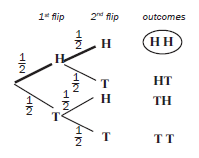
The tree diagram shows 4 outcomes.
Each time you flip the coin, the outcomes (heads or tails) do not depend on the outcomes of the last flip. So these events are independent of each other.e.g.8
You have a pack of cards (no jokers).
What is the probability of these two events?
- Event A: Drawing a heart card from a pack of cards and putting it back.
- Event B: Drawing a heart card from the pack again.
A and B are independent events. No matter what card is drawn in Event A, it is put back in the pack. So the outcome of event B does not depend on the outcome of event A.
Tree diagram
Here is the tree diagram for all possible outcomes of the two events.
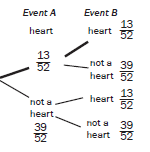
Outcomes for heart then heart
13 x 13 = 1 x 1 = 1
52 52 4 4 16
P(A and B) =1/16
Compare this with:
P(A) × P(B) = –¼ –¼ = 1/16
∴ P(A and B) = P(A) × P (B)Events are independent if the probability of one event happening is not influenced by another event happening. P(A and B) = P(A) × P(B)……..if the events are independant - Dependent events
Two successive events are dependent if the outcomes of the one event influence the outcomes of the other event.
e.g.9
What is the probability of these two events?
- Event A: Drawing a heart from a regular pack of cards and not putting it back.
- Event B: Drawing a heart again, from the rest of the pack (51 cards left).
| Solution A and B are dependent events, because event B depends on the outcomes of event A. Here is a tree diagram for Event A and Event B.  Outcomes for heart then heart 13 x 12 = 156 x = 1 52 51 2652 17 P(A and B) =1/17 Compare this with: P(A) × P(B) = ¼ x ¼ = 1/16 ∴ P(A and B) ≠ P(A) × P (B) When the events are dependent. |
| Events are dependent if the probability of one event happening is influenced by how another event happens. P(A and B) ≠ P(A) × P(B)…………. for dependant events |
8.9 Contingency tables
We can also use a contingency table to represent all possible outcomes of events.
Look at the same example we used for the tree diagram above:
What is the probability of these two events?
- Event A: Drawing a heart card from a pack of cards and putting it back.
- Event B: Drawing a heart card from the pack again.
We can make a table of possible outcomes using columns for the type of card drawn and rows for the events:
| heart | not heart | Total | |
| Event A | 13 | 39 | 52 |
| Event B | 13 | 39 | 52 |
| Total | 26 | 78 | 104 |
| Numbers in each row add up to totals on the right. Numbers in each column add up to totals below the table. |
e.g.10
The hair colour of 50 learners was recorded. The table below represents the information
| Girls | Boys | Total | |
| Black | 10 | 12 | 22 |
| Brown | 8 | 9 | 17 |
| Blond | 6 | 5 | 11 |
| Total | 24 | 26 | 50 |
Calculate the probability that learner chosen at random:
- will have brown hair
- will have blond hair
- will have black hair or brown hair
- will have blond hair or brown hair or black hair
Solutions
|
Activity 4
- P(A) = 0,45; P(B) = 0,3 and P(A or B) = 0,165.
Are the events A and B:- mutually exclusive
- independent (7)
- What is the probability of throwing at least one six in four rolls of a regular die? (3)
- What is the probability of throwing four 6s in a row with four rolls of a regular die? (3)
- If two dice are rolled at the same time, what is the probability that the sum of the two numbers is 9? (3)
[16]

Solutions
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
8.10 Counting principles
Statistics has many applications in everyday life. The tree diagrams and contingency tables used so far are useful if there are not too many outcomes or possibilities. Look at these examples.
e.g.11
- How many different outfits can be combined using a shirt and a pair of pants from 3 shirts (red, white or blue) and 2 pairs of pants (black or brown)?
SHIRTS: red; white and blue
PANTS: black and brownSolution
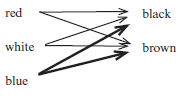
Outcomes:
red/black red/brown white/black
white/brown blue/black blue ∴ 6 different outfits (3 × 2 = 6)
brown - How many different meals could you have if the menu at a restaurant offered:
Dinner Drink Dessert
fried chicken orange juice ice cream
fish and chips Coca-Cola apple pie
hamburger coffee
teaSolution
We can use 3 × 4 × 2 = 24 to find the number of different meals.
We need a more effective way of counting and keeping track of all
possibilities.
- Counting permutations
The number of permutations of n different items
e.g.12
How many different ways could you arrange 4 books on a shelf ?
Call them P, Q, R and S.
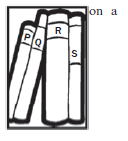
There are 6 possible outcomes that start with P:
P Q R S
P Q S R
P R S Q
P R Q S
P S R Q
P S Q R
Now start with Q (6 possibilities)
Now start with R (6 possibilities)
Now start with S (6 possibilities)
(24 different ways to arrange 4 books)
Instead of writing down all the possibilities, we can find the answer by using the factorial (!) key on a calculator.
4! = 4 × 3 × 2 × 1 = 24Using n factorial (n!):
The exclamation mark ! is called the factorial symbol.
4! reads as ‘four factorial’ and means 4 × 3 × 2 × 1
7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5 040 - Permutations of outcomes that are not all distinct (some are the same)
e.g.13
Consider the word TAN
How many word arrangements can be made with the word TANSolution
There are three letters. Possible words are:
TAN TNA ANT ATN NTA NAT
3!=3
Permutation: A way of grouping elements of a group in a specific order.
e.g.14 Consider the word MOM
How many word arrangements can be made with the word MOM if the repeated letters are treated as different letters?
How many word arrangements can be made with the word MOM if the repeated letters are treated as the same letters.
Solutions
|
Activity 5
- Determine the number of permutations that can be formed from all the letters of the word ABRACADABRA. (4)
- Determine the number of permutations that can be formed from all the letters of the word ABRACADABRA. This time, the first and last letters must be A. (4)
- Determine the number of permutations that can be formed from all the letters of the word ABRACADABRA. This time, all the As have to be next to each other. (4)
[12]
Solutions
|
C) T he number of permutations of m distinct objects taken n at a time
e.g.15
There are 6 people in a room. Call them A, B, C, D, E and F.
How many different groups of 2 people are possible?
| Solution The question is really – how many permutations of 2 people (A to F) are possible? We can list them: AB AC AD AE AF (5) or BA CA DA EA FA (5) BC BD BE BF (4) or CB DB EB FB (4) CD CE CF (3) or DC EC FC (3) DE DF (2) or EC FD (2) EF (1) or FE (1) There are 5 + 4 + 3 + 2 + 1 + 5 + 4 + 3 + 2 + 1 = 30 different groups of 2 people. |
To find this answer without writing all the possibilities out, we can use the formula:
| Permutations: mPn = m! (m–n)! where m = total number of possibilities n = number of items chosen in a group |
So 6P2 = 6! = 6! = 6×5×4×3×2×1 = 6 × 5 = 30
(6-2)! 4! 4x3x2x1
Use the factorial key on the calculator, or work it out as shown here.
D) T he number of permutations of m items taken n at a time (where the items may be repeated any number of times)
e.g.16
In a multiple choice test there are 5 questions, each with 4 multiple choice answers. How many possible ways are there of answering the questions if you guess the answers?
| Solution Since you can choose from 4 answers for each question, you can represent the answers with 5 ‘boxes’ of 4 solutions: 4 × 4 × 4 × 4 × 4 = 45 = 1 024 |
e.g.17
How many three digit numbers can be formed with the digits 0 – 9, if numbers can be repeated?
| Solution 10 ‘boxes’ of 3 numbers: 10 × 10 × 10 = 103 = 1 000 |
SUMMARY
The basic counting principle:
The number of ways of making several decisions in succession (call them m1; m2 and m3 etc…) is determined by multiplying the numbers of choices that can be made in each decision. m1 × m2 × m3 …
Permutations
- The number of permutations of m different items is m!
- The number of permutations of m items of which:
a are alike, b are alike, c are alike is: m!
a! × b! × c! - The number of permutations of m items taken n at a time, when each of the items may be repeated any number of times, is:
m × m × m × m × … to n factors = mn times. - The number of ways that m items taken n at a time can be arranged, is mPn = m!
(m-n)!
Activity 6
- At Angelo’s pizza place you can choose from 6 different types of pasta and 28 different sauces. How many different meals of 1 type of pasta and 1 type of sauce can you have? (2)
- In how many different ways can we arrange 7 books on a shelf ? (2)
- In how many different ways can 9 girls sit on one side of a table? (2)
- In how many ways can a three-letter word be made from the letters c; d; e; f without repeating any letters? (3)
- How many possible choices can be made in a multiple choice quiz if there are 4 questions each with 3 answers? (3)
- How many different words can be made using the letters from LIMPOPO? (4)
- How many 3-digit numbers can be made with the digits 1 – 5 if:
- repetitions are allowed (2)
- repetitions are not allowed (3)
- A code is made using the format XYY, where the X is any letter in the alphabet and Y represents any digit from 0 to 9.
- How many possible codes can be formed if the letters and digits are repeated? (3)
- How many possible codes can be formed if the letters and digits are not repeated? (3)
[27]
Solutions
|
8.11 Use of counting principles in probability
e.g18
- What is the probability that a random arrangement of the letters of BAFANA starts and ends with an ‘A’?
- A drawer contains 20 envelopes. 8 of the envelopes each contain 5 blue and 3 red sheets of paper. The other 12 envelopes each contain 6 blue and 2 red sheets of paper. One envelope is chosen at random. A sheet of paper is chosen at random from it. What is the probability that this sheet of paper is red?
Solutions
|
What you need to be able to do:
- Revise the addition rule for mutually exclusive events: P (A or B) = P (A) + P (B)
- Revise the complementary rule: P(A′) = 1 – P (A)
- Revise the identity P (A or B) = P (A) + P (B) – P (A and B) for all probability events.
- Identify dependent and independent events and use the product rule
- Use Venn diagrams to solve problems for up to three events.
- Introduce an x for an event to solve problems.
- Use tree diagrams and contingency tables for probability of consecutive events or simultaneous events which are not necessarily independent.
- Understand and use Counting principles in probability.

 (4)
(4)
 (4)
(4)





