Activity 1
- Given the sequence 6; 13; 20; …
- Determine a formula for the nth term of the sequence.
- Calculate the 21st term of this sequence.
- Determine which term of this sequence is 97. (5)
- Consider this number pattern: 8; 5; 2; …
- Calculate the 15th term.
- Determine which term of this sequence is –289. (4)
- Given the arithmetic sequence 1 − p; 2p − 3; p + 5; . . . determine the value of p.
- Determine the values of the first three terms of the sequence. (5)
[14]
| Solutions
- It is an arithmetic sequence because there is a common difference.
a = 6; d = 7 Tn = a + (n – 1)d
Tn = 6 + (n – 1)(7)
Tn = 7n – 1 - T21 = 7(21) – 1 = 147 – 1 = 146
- 97 = 7n – 1
∴98 = 7n
∴14 = n
∴97 is the 14th term of the sequence. (5)
- It is an arithmetic sequence: a = 8; d = 5 – 8 = 2 – 5 = – 3
Tn = a + (n – 1)d
∴T15 = 8 + (15 – 1)(–3)
T15 = 8 + 14(–3)
T15 = 8 – 42 = –34 - Tn = a + (n – 1)d
– 289 = 8 + (n – 1)(–3)
∴– 289 = 8 – 3n +3
∴– 300 = –3n
∴100 = n 3 ∴– 289 will be the 100th term (4)
- Since this is an arithmetic sequence, you can assume that there is a common difference between the terms.
d = T2 – T1 = T3 − T2
∴(2p – 3) – (1 – p) = ( p + 5) – (2p – 3)
3p – 4 = – p + 8
4p = 12 - p = 3
T1 = 1 – p = 1 – 3 = –2
T2 = 2p – 3 = 2(3) – 3 = 3
T3 = p + 5 = 3 + 5 = 8
So the first three terms of the sequence are –2; 3; 8 (5)
[14]
|
Activity 2
- Consider the number pattern: 3; 13; 31; 57; 91; …
- Determine the general term for this pattern.
- Calculate the 7th term of this pattern.
- Which term is equal to 241? (9)
- Find term 6 of this pattern and then find the rule in the form
Tn = an2 + bn + c
–1 ; 3; 9; 17; 27 … (4)
[13]
Solutions- It helps to make a diagram:
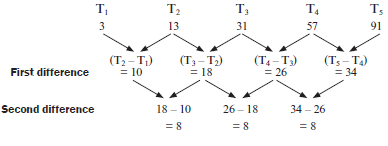
∴ it is a quadratic sequence.
2a = 8 ∴ a = 4
3a + b = 10 ∴3(4) + b = 10
b = –2
a + b + c = 3 ∴ 4 + (–2) + c = 3
c = 1
∴Tn =4n2 – 2n + 1 - T7 = 4(7)2 – 2(7) + 1
= 4(49) – 14 + 1
= 183 - 241 = 4n2 – 2n + 1
0 = 4n2 – 2n + 1 – 241 make the equation = 0 to solve
0 = 4n2 – 2n – 240
0 = 2n2 – n – 120 divide through by 2
0 = (2n + 15)(n – 8)
factorise
∴ 2n + 15 = 0 OR n – 8 = 0
∴ n = –7,5 OR n = 8 3 (9)
- T1 T2 T3 T4 T5
–1 3 9 17 27 …
4 6 8 10
2 2 2
∴T6 = 27 + (10 + 2) = 39 3 use the pattern of the numbers
2a = 2 ∴a = 1
3a + b = 4
3(1) + b = 4 ∴ b = 1
a + b + c = –1
1 + 1 + c = –1 ∴ c = –3
Tn = n2 + n – 3 (4)
[13]
|
n = –7,5 not possible because n is the position of the term so it must be a positive natural number. ✓
∴ 241 is the 8th term of the sequence.
Activity 3
- Determine the 10th term of the sequence: 3; 6; 12; . . . (2)
- Determine the number of terms in the sequence: 2; 4; 8; . . .; 1024 (2)
- If 5; x; 45 are the first three terms of a geometric sequence, determine the value of x. (2)
- Determine the geometric sequence whose 8th term is 9 and whose 10th term is 25. (3)
[9]
Solutions- a = 3; r = 6/3 = 12/6 = 2
Tn = arn−1
T10 = 3(2)10−1 = 3(2)9 = 3 × 512 = 1536 (2) - a = 2; r = 4/2= 8/4 = 2
arn–1 = 1024
2(2)n–1 = 210 = 2n = 210
∴ n = 10 (2) - x/5 = 45/x
x = ± √225 = ± 15 (2) - ar7 = 9
ar9 = 25
ar9 = 25
ar7 9
∴r2 = 25/9
r = 5/3
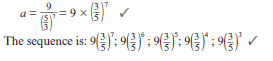
[9]
|
Activity 4
- Determine the sum of the series: 19 + 22 + 25 + . . . + 121 (3)
- The sum of the series 22 + 28 + 34 + . . . is 1870. Determine the number of terms. (2)
- Given the arithmetic sequence -3; 1; 5; …,393
- Determine a formula for the nth term of the sequence.
- Write down the 4th, 5th, 6th and 7th terms of the sequence.
- Write down the remainders when each of the first seven terms of the sequence is divided by 3.
- Calculate the sum of the terms in the arithmetic sequence that are divisible by 3. (10)
- The sum of n terms is given by Sn = n/2 (1 + n) . Determine T5. (3)
- 3x + 1; 2x; 3x − 7 are the first three terms of an arithmetic sequence. Calculate the value of x. (3)
- The first and second terms of an arithmetic sequence are 10 and 6 respectively.
- Calculate the 11th term of the sequence.
- The sum of the first n terms of this sequence is –560. Calculate n. (6)
[27]
| Solutions
- a = 19 and d = 3
Tn = 3n + 16 = 121
3n = 105
n = 35
Sn = n/2(a + l)
S35 = 35/2 (19 + 121) = 35/2 (140) = 35 × 70 = 2450 (3) - a = 22 and d = 6
Sn = n/2 [2a + (n − 1)d] n
n/2 [2 × 22 + (n − 1)6] = 1870
19n + 3n2 = 1870
3n2 + 19n − 1870 = 0
(3n + 85)(n − 22) = 0 3
∴ n = 22
n cannot be a negative because it is the number of terms (2) - Tn = –3 + (n − 1)4
4n – 7 = Tn - T4 = 5 + 4 = 9; T5 = 9 + 4 = 13; 3 T6 = 13 + 4 = 17 and
T7 = 17 + 4 = 21 - 0; 1; 2; 0; 1; 2; 0
- Tn = –3 + 12 (n − 1)
393 = 12n – 15
12n = 393 + 15 = 408
n = 34
S34 = 34/2 × (–3 + 393)
= 17 × 390
= 6630 (10)
- S5 = 5/2 ( 1 + 5 ) = 15
S4 = 4/2 ( 1+ 4 ) = 10
T5 = 15 – 10 = 5 (3) - T2 – T1 = T3 – T2
2x – (3x + 1) = (3x – 7) – 2x
2x – 3x – 1 = 3x – 7 – 2x
–2x + 6 = 0
2x = 6
x = 3 (3) - Tn = a + (n – 1)d
T11 = 10 + (11 – 1)(–4)
= –30 - Sn =n/2 [2a + (n – 1)d]
–560 = n/2 [2(10) + (n – 1)(–4)]
–1120 = –4n2 + 24n
4n2 – 24n – 1120 = 0
n2 – 6n – 280 = 0
(n – 20)(n + 14) = 0
n = 20 or n = –14
n = 20 only because number of terms cannot be a negative number (6)
[27]
|
Activity 5
- Determine 3 + 6 + 12 + 24 + . . . to 10 terms (2)
- If 2 + 6 + 18 + . . . = 728, determine the value of n. (3)
[5]
Solutions- a = 3 and r = 6/3 = 12/6 = 2
Sn = a( r n − 1)
r – 1
S10 = 3( 2 10 − 1) = 3(1024 − 1) = 3069 (2)
2 – 1 - a = 2 and r = 6/2 = 18/6 = 3
Sn = 2(3n − 1) = 728
3 – 1
2(3n − 1) = 728
2
3n − 1 = 728
3n = 729 = 36
∴ n = 6 (3)
[5]
|
Activity 6

Look for two different sequences in the pattern and separate them
Solutions- The question asks you to find the sum of the terms from n = 4 to
n = 70 if the nth term is 2n – 4.
a = T1 = 2(4) – 4 = 4 Find the first term a
T2 = 2(5) – 4 = 6
T3 = 2(6) – 4 = 8
So the sequence is 4; 6; 8; … and this is an arithmetic series.
To check d, calculate T2 – T1
d = T2 – T1 = 6 – 4 = 2
n = (70 – 4) + 1 = 67 There are 67 terms
Now we can substitute these values into the formula to find the sum of 67 terms.
Sn = n/2 [2a + (n – 1)d]
S67 = 67/2 [2(4) + (67 – 1)2]
S67 = 33.5 [8 + 132] = 4690
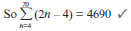
(3) - This is a geometric series because 5(3)k–1 has the form ark–1, T1 = 5(3)1–1 = 5 ;
T2 = 5(3)2–1 = 15; T3 = 5(3)3–1 = 45
a = 5; r = 3; n = m and Sm = 65
Sn = a( rn −1)… substitute
r – 1
65 = 5(3m − 1) … multiply through by 2
2
65 = 5(3m − 1)
2
130 = 5.3m – 5 … add like terms
135 = 5.3m … divide through by 5
27 = 3m … write 27 as a power of 3
33 = 3m … bases are the same, so the powers are equal
∴ m = 3 (4) - T1, T3 and T5 form a sequence with a common ratio of ½, so T7 is 1/16 .
T2, T4 and T6 form a sequence with a common difference of 3, so T8 is 13. - S50 = 25 terms of 1st sequence + 25 terms of 2nd sequence
S50 = ( ½ + ¼ + 1/8 + … to 25 terms) + (4 + 7 + 10 + 13 + … to 25 terms)
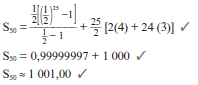
(5)
[12] |
Activity 7
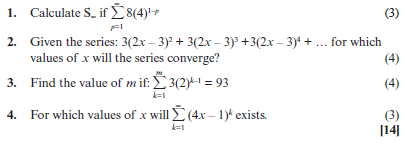
Solutions- T1 = 8(4)1 – 1 = 8 = a
To find r, find the common ratio using T1 and T2, T2 and T3.
T2 = 8(4)1 – 2 = 8(4)–1 = 8 × ¼ = 2
T3 = 8(4)1 – 3 = 8(4)–2 = 8 × 1/16 = ½
T2 ÷ T1 = 2/8 = ¼ and T3 ÷ T2 =½ = ½ x ½ = ¼
2
so r = ¼ and a = 8
∴S∞ = a = 8 = 8
1 – r 1 – ¼ 3/4
= 8 x 4/3 = 32/3
When dividing by a fraction, you can multiply by the inverse
∴S∞ = 32/3 or 102/3 (3) - This is a geometric series with r = 2x – 3
To converge –1 < r < 1
–1 < 2x – 3 < 1 Add 3 to both sides
2 < 2x < 4 Divide by 2 on both sides
1 < x < 2 3 x ≠ 3/2 (4)
The series will converge for 1 < x < 2 - a = 3; r = 2; Sm = 93
Sn = a(1 − r n )
1 – r
93 = 3 (1 − 2m )
1 – 2
93 = 3( 1 − 2m)
– 1
–93 = 3(1 – 2m)
–31 = 1 – 2m
2m = 32
2m = 2 5
∴ m = 5 (4) - r = 4x – 1
–1 < r < 1
-1 < 4x -1 < 1; x ≠ ¼
0 < 4x < 2
0 < x < ½ (3)
[14]
|





