Euclidean Geometry Mathematics Grade 12 Notes and Study Guides free. The study of plane and solid figures on the basis of axioms and theorems employed by the Greek mathematician Euclid (c. 300 BCE). In its rough outline, Euclidean geometry is the plane and solid geometry commonly taught in secondary schools. Indeed, until the second half of the 19th century, when non-Euclidean geometries attracted the attention of mathematicians, geometry meant Euclidean geometry.
It is the most typical expression of general mathematical thinking. Rather than the memorization of simple algorithms to solve equations by rote, it demands true insight into the subject, clever ideas for applying theorems in special situations, an ability to generalize from known facts, and an insistence on the importance of proof.
In Euclid’s great work, the Elements, the only tools employed for geometrical constructions were the ruler and the compass—a restriction retained in elementary Euclidean geometry to this day.
EUCLIDEAN GEOMETRY GRADE 12 NOTES – MATHEMATICS STUDY GUIDES
12.1 Revise: Proportion and area of triangles
1. Ratio and proportion
Ratio compares two measurements of the same kind using the same units.
Example
If Line A is 2 units long and Line B is 6 units long, then the ratio of Line A : Line B is 2 : 6.
This is the same ratio as 1 : 3. Line C is 1 unit long and Line D is 3 units long.
So Line C : Line D is 1 : 3. So C and D are in the same proportion as A and B.

So the two ratios are equal and we can say that A/B = C/D
We say that A, B, C and D are in proportion.
This proportion can be written in many ways:
If A/B = C/D , then 1. A/C = B/D 2. A/B = D/C 3. C/A = D/B
Ratio and proportion of areas and sides of triangles
- If two or more triangles have a common vertex (A) and lie between the same parallel lines, they also have a common perpendicular height (altitude).
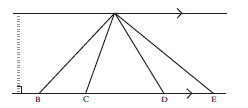
- The areas of triangles with equal altitudes are in the same proportion as their bases.
Remember: area ∆ = ½ base × perp height
∆ADB, ∆DBC and ∆ADC all have the same ⊥ height DE.
So Area ∆ADB : Area ∆DBC : Area ∆ADC
(½ AB × DE) : (½ BC × DE) : (½ AC × DE) AB : BC : AC
- If two or more triangles lie between parallel lines, they have the same altitude.
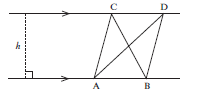
- Triangles on the same base (or equal bases) and between parallel lines are equal in area.
Area ∆ABC = ½(AB)h
Area ∆ADB = ½(AB)h
Area ∆ABC = Area ∆ADB
12.2 Proportion theorems
Theorem 7 (Learn the proof for the examination)
Proportional Theorem
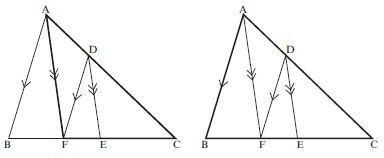
If a line is drawn parallel to one side of a triangle, it divides the other two sides in the same proportion.
(Prop theorem, DE ∣∣ BC)

Given: Triangle ABC with D on AB and E on AC, DE ∣∣ BC
To prove: AD/DB = AE/EC
Proof: Construction: Draw altitudes h and k in ∆ADE
Join DC and BE
Area of ΔADE = ½.AD.h = AD (same altitude h)
Area of ΔBDE ½.DB.h DB
and Area of ΔADE = ½.AE.k = AE (same altitude k)
Area of Δ CED ½.EC.k EC
but Area ∆ADE = Area ∆CED (same base DE; same altitude; DE ∣∣ BC)
∴ Area of ∆ADE = Area of ∆ADE
Area of ∆ BDE Areaof ∆ CED
∴ AD/DB = AE/EC
Solving problems using proportion
Activity 1
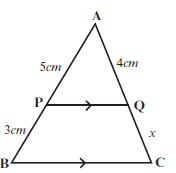
- Determine the value of x, in the diagram alongside, if PQ ∣∣ BC. (4)
Solution
AP = AQ (PQ ∣∣ BC, prop theorem)
PB QC
∴ 5/3 = 4/x
∴ 5x = (3)(4)
∴ x = 12/5 = 2,4 cm 3 [4] - In ∆ABC, AB ∣∣ FD; AF ∣∣ DE and FE : EC = 3 : 4.
Determine EC : BF (7)
NOTE:
3 : 4 does not mean that
FE = 3 and EC = 4.
For any a, we can say that
FE = 3a and EC = 4a
For every 3 of a in FE, there is
4 of a in EC.Solution
Work with two different triangles:
∆ACF and ABC
In ∆ACF:
AD = FE (AF ∣∣ DE, prop intercept theorem)
DC EC
In ∆ABC:
AD = BF (AB ∣∣ FD, prop intercept theorem)
DC FC
∴ FE = BF(both = AD)
EC FC DC
FE = 3a and BF = BF
EC 4a FC 7a
∴ 3a = BF
4a 7a
∴ BF = 3(7a/4) = 21a____4
∴ EC = 4a ÷ 21a/4
BF
= 4a × 4
1 21a
= 16
21
∴ EC : BF = 16 : 21 [7] - Determine the value of x if PQ ∣∣ BC. (4)
Solution
AP = AQ (prop theorem , PQ ∣∣ BC)
PB QC
5/3 = 4/x
5x = (3) (4)
x = 12/5 = 2,4cm
[4] - In the diagram, RF ∣∣ KG , ED ∣∣ KH,
RH = 3 units, RK = 9 units, HF = 2 units. GE: EK = 1:3
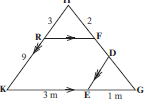
Calculate (stating reasons) the lengths of:
4.1 FG
4.2 FD (8)Solutions
4.1
In ∆HKG
FG = 9 S (line ∣∣ one side of a ∆) 3 R or (RF ∣∣ KG)
2 3
FG = 6 units S (3)
4.2 GD = GE = ¼ S (line ∣∣ one side of a ∆) 3 R or (ED ∣∣ KH)
GH GK
GD = ¼ .GH
GD = ¼ .(8) S
GD = 2 S
∴ FD = 6 − 2 = 4units 3 R
OR
In ∆HKG, HK ∣∣ DE
GD = EG = 1/3 S
DH EK
(line ∣∣ one side of a ∆) R or (proportional theorem, HK//DE )
6 − FD = 1/3 S
2 + FD
18 − 3FD = 2 + FD
∴ FD = 4 units (5)
[8]
12.3 Similar polygons
Similar polygons have the same shape, but not necessarily the same size.
e.g.1
Every square is similar to every other square.

Polygons (with the same number of sides) are similar when:
- All the pairs of corresponding angles are equal (They are equiangular)
and - All the pairs of corresponding sides are in the same proportion.
Both of these conditions must hold at the same time.
||| is the symbol we use to say one polygon ‘is similar to’ another polygon.
e.g.2

Corresponding sides are sides in the same position (with respect to the angles) in each polygon.
Consider pentagon ABCDE and pentagon PQRST
^A = ^P ; ^B = ^Q ; ^C = ^R ; ^D = ^S ; ^E = ^T
AND
AB = BC = DC = ED = EA
PQ QR SR TS TP
∴ABCDE ||| PQRST (equiangular and corresponding sides in the same proportion)
Triangles are special polygons:
- If two triangles are equiangular, then their sides will always be in the same proportion, so the triangles are similar.
- If the sides of two triangles are in the same proportion, then the triangles will be equiangular, so the triangles are similar.
equiangular ∆s ➝ similar ∆s
corresponding sides ∆s in
proportion ➝ ∆s are similar
Theorem 9 (Learn the proof for the examination)
If two triangles are equiangular, then the corresponding sides are in proportion and therefore the triangles are similar.
Given: ∆ ABC and ∆ DEF with ^A = ^D ; ^B = ^E ; =^F
To prove: DE = EF = DF
AB BC AC
Proof: On AB mark off AP = DE and on AC mark off AQ = DF
Draw PQ
In ∆ APQ and ∆ DEF
AP = DE (Construction)
^A = ^D (given)
AQ = DF (Construction)
∴ ∆ APQ ≡ ∆ DEF (SAS)
∴ ^P1 = ^E
∴ ^P1 = ^B (^E = ^B)
∴ PQ ∣∣ BC (Corresponding ∠s equal)
∴ AP = AQ
AB AC
(PQ ∣∣ BC in ∆ ABC )
But AP = DE and AQ = DF
∴ DE = DF
AB AC

Similarly, we can prove that
DE = EF
AB BC
∴ DE = EF = DF
AB BC AC
But the triangles are equiangular
∴ ∆ ABC ||| ∆ DEF
| NOTE: If two triangles have 2 corresponding angles equal, then the third angles will equal each other (sum angles of a triangle = 180°) and the triangles are therefore similar and their sides will be in proportion. The shortened reason you can use is (third angle)  If two angles are the same, then the 3rd angle of both triangles is 180° – (40° + 80°) (sum angles in ∆) = 60° |
Theorem 10 (Learn the proof for the examination)
If two triangles have their sides in the same proportion, then the corresponding angles will be equal and the triangles are similar.
Given: ∆ABC and ∆ DEF with DE = EF = DF
AB BC AC
To prove:
^A = ^D ;^B = ^E ;^C = ^F
Proof: Draw ∆ PEF so that
PEF =^B and EFP = ^C
∴ ∆PEF ||| ∆ABC (equiangular ∆s)
∴ PE = EF = PF
AB BC AC
But DE = EF = DF
AB BC AC
(Given)
∴ PE = ED and PF = DF
and EF is common
∴ DEF ≡ ∆ PEF (SSS)
∴ ^F1 = ^F2 = ^C
and
^E1= ^E2 = ^B
i.e.
^A =^D ;^B =^E1 ; ^C =^F 1
But the corresponding sides of the triangles are proportional
∴ ∆ ABC ||| ∆DEF

Theorem 11 (Learn the proof for the examination)
Theorem of Pythagoras (proved using similar triangles)
In any right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
Given: ∆ABC with ^A = 90°
To Prove: BC2 = AB2 + AC2
Proof: Draw AD ⊥ BC
In ∆ABD and ∆CBA
^B is common
ADB = CAB = 90° (given)
BAD = BCA (3rd ∠ of ∆)
∴ ∆ABD ||| ∆CBA (AAA)
∴ AB = BD
BC AB
(ABD ||| CBA)
∴ AB2 = BC × BD
Similarly ∆ACD ||| ∆CBA and AC2 = DC × CB
∴ AB2 + AC2 = BC × BD + DC × CB
AB2 + AC2= BC (BD + DC)
AB2 + AC2 = BC × BC
AB2 + AC2 = BC2

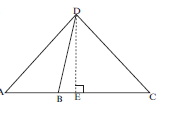
Activity 2
- Diameter AME of circle with centre M bisects FAB.
MD is perpendicular to the chord AB.
ED produced meets the circle at C, and CB is joined.
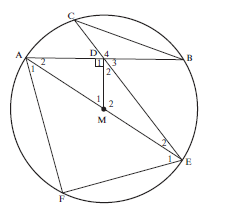
- Prove ∆AEF ||| ∆AMD (5)
- Hence, find the numerical value of AF. (5)
AD - Prove ∆ CDB ||| ∆ADE (4)
- Prove AD2 = CD. DE (3)
[17]Solution a)
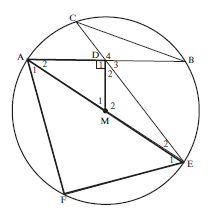
F = 90° (∠ in semi-circle)
^D1 = 90° (given MD ⊥ AB)
∴ ^F = ^D1
In ∆AEF and ∆AMD
^F = ^D1 (proved)
^A1 = ^A2 (AM bisects FAB)
∴ ^E1 = ^M1 (third ∠ of ∆)
∴ ∆AEF ∣∣∣ ∆AMD (AAA) or ∠∠∠ (5)Solution
b) AE = EF = AF (||| ∆s)
AM MD AD
AM = ME (radii)
∴ AE = 2AM
∴ 2AM = AF
AM AD
∴ AF = 2 (5)
ADc)
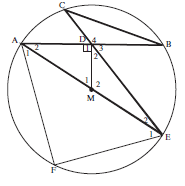
In ∆CDB and ∆ADE
^C = ^A2 (∠s in same seg)
^B = ^E2 (∠s in same seg)
^D4 = ^D1 + ^D2 (opp ∠)
∴ ∆CDB ||| ∆ADE (AAA) (4)Solution
d)
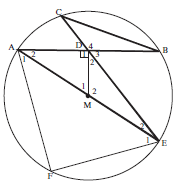
CD = DB (III ∆s)
AD DE
∴ CD.DE = AD.DB
But AD = DB (MD ⊥ AB, M is centre)
∴ CD. DE = AD
∴ AD2 = CD.DE (3)
[17]
- CD is a tangent to circle ABDEF at D.
Chord AB is produced to C. Chord BE cuts chord AD in H and chord FD in G. AC ∣∣ FD and FE = AB
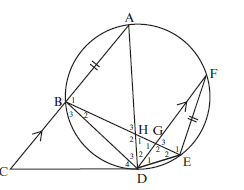
- Prove that ^D4 = ^D2 (3)
- Prove that ∆BHD ||| ∆FED (5)
- Hence AB = FD (3)
BH BDSolutions
a) ^A = ^D4 (tan-chord thm)
^D2 = ^A (alt ∠s CA ∣∣ DF)
^D4 = ^D2 (3)
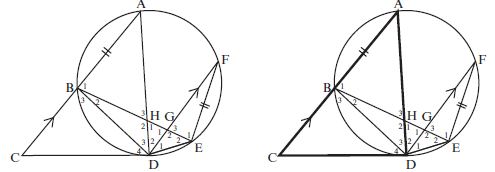
b) In ∆BHD and ∆FED
^B2 = ^F(∠s in same seg)
^D3 = ^D1 (equal chords)
^H2 = ^E2 (third ∠ of Δ)
∴ ∆BHD ||| ∆FED ∠∠∠ (5)c) FE = FD (||| ∆s)
BH BD
But FE = AB (given)
∴ AB = FD (3)
BH BD
[11][11]
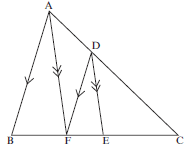
- In the diagram ∆ABC is such that F is on AB and G is on AC. CB is produced to meet GF produced at E .DGFE is a straight line. BFA ∣∣ CD.
AB = 20, BC = 10, EF = 8, EB = 5 and FB = 6.
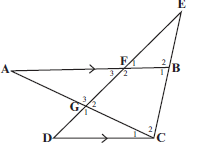
3.1 Determine the numerical value of EF (3)
ED
3.2 Calculate the length of ED (2)
3.3 Complete, without stating the reasons: ∆EFB III ∆ …. (1)
3.4 Hence, calculate the length of DC (3)
3.5 Prove that: AF = FG(4)
CD DG
[13]Solutions
BFA ∣∣ CD. AB = 20, BC = 10, EF = 8, EB = 5 and FB = 6
3.1 FB ll CD (Given) EF = EB S (line ∣∣ one side of A) 3 R
ED EC
EF = 5 = 1 S (3)
ED 15 3
3.2 EF = 1 from 3.1 and EF = 8
ED 3
∴ 8 = 1
ED 3
ED = 24 S (2)
3.3 ∆EFB ∣∣∣ ∆EDC (1)
3.4 DC = ED (∆EFB ∣∣∣ ∆EDC) R
FB EF
DC = 24 S
6 8
DC = 18 S (3)
3.5 In ∆AFG and ∆CDG
^A = ^C1 (alt ∠s. AF ∣∣ DC) S/R
^G3 = ^G1 (vertically opp ∠s) S/R
^F = ^D (alt ∠s. AF ∣∣ DC)
∆ AFG III ∆CDG (∠∠∠) R
AF = FG (∆AFG ∣∣∣ ∆CDG) 3 R (4)
CD DG
[13] - In the diagram, PQCB is a cyclic quadrilateral. Chords BP and CQ are produced to meet at A such that AQ = BC.
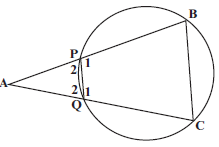
4.1 Prove that: ΔAPQ III ΔACB (4)
4.2 Hence, prove that AQ² = AB.PQ (3)
[7]Solutions
4.1 Proof: In ΔAPQ and ΔACB
^A = ^A (common) S/R
^P2 = ^C S (ext ∠ of a cyclic quad ) 3 R
^P2 = ^ B (sum ∠s of ∆) or ( ext ∠ of cyclic quad )
∆APQ ∣∣∣ ∆ACB ( ∠.∠.∠) R (4)
4.2 AQ = PQ S (∆APQ ∣∣∣ ∆ACB) S
AB BC
AQ = PQ S ( AQ = BC )
AB AQ
AQ2 = AB.PQ (3)
[7]
















