Algebra Questions and Answers Mathematics Grade 12. Algebra is the part of mathematics that helps represent problems or situations in the form of mathematical expressions. In algebra, we use numbers like 2, −7, 0.068 etc., which have a definite or fixed value. In algebra we use variables like x, y, and z along with numbers
Activity 1
Factorise each of the following completely:
- 12x2 + 17x + 6
- 5x2 – 23x – 10
- 9x2 + 5x – 4
- 12x2 – 11x + 2
- 5x2 – 45
- 2x3 + 16
- 6x3 – 13x2 + 5x
[16]
| Solutions
- 12x2 + 17x + 6
= 12x2 + 9x + 8x +6………..12 × 6 = 72 and 72 = 9 × 8 (9 + 8 = 17)
= 3x(4x + 3) + 2(4x + 3)
= (4x + 3)(3x + 2) (2) - 5x2 – 23x – 10
= 5x2 – 25x + 2x – 10…………5 × –10 = –50 and 50 = 25 × 2 (–25 + 2 = –23)
= 5x(x – 5) + 2(x – 5)
= (x – 5)(5x + 2) (2) - 9x2 + 5x – 4
= 9x2 + 9x – 4x – 4…………..9 × –4 = –36 and 36 = 9 × 4 (9 – 4 = 5)
= 9x(x + 1) – 4(x + 1)
= (x + 1)(9x – 4) (2) - 12x2 – 11x + 2
= 12x2 – 3x – 8x + 2…………..12 × 2 = 24 and 24 = 8 × 3 (–8 – 3 = –11)
= 3x(4x – 1) – 2(4x – 1)
= (4x – 1)(3x – 2) (2) - 5x2 – 45……………………….Common factor of 5
= 5(x2 – 9) ……………………….Difference of two squares
= 5(x – 3)(x + 3) (2) - 2x3 + 16……………………….Common factor of 2
= 2(x3 + 8) ……………………….Sum of two cubes
= 2(x + 2)( x2 – 2x + 4) (3) - 6x3 – 13x2 + 5x……………………….Common factor of x
= x(6x2 – 13x + 5) 3……………………….Trinomial factorising
= x(6x2 – 3x – 10x + 5) ………….. 6 × 5 = 30 and 30 = 10 × 3 (–3 – 10 = –13)
= x[3x(2x – 1) – 5(2x –1)]
= x[(2x – 1)(3x – 5)] (3)
[16]
|
Activity 2
Solve for x:
- x(x + 3) = 0
- x(2x – 5) = 12
- 2x2 + x − 6 = 0
- 2x2 = 32
- 3x + 1/x = 4, x ≠ 0
- 2√x − 3 = x − 3
[22]
If (A) × (B) = 0, then either A = 0 OR B = 0.
| Solutions
- x(x + 3) = 0 We have a product = 0. Therefore put each factor = 0
x = 0 or x + 3 = 0
x = 0 3 or x = –3 (2) - x(2x – 5) = 12 We need a product = 0. Therefore, multiply out brackets and write in standard form with all the terms on one side and equal to 0
(2x + 3)(x – 4) = 0 Factorise
2x + 3 = 0 or x – 4 = 0 Put each factor = 0
2x = –3 or x = 4
x = -3/2 x = 4 (2) - 2x2 + x − 6 = 0
(2x − 3)(x + 2) = 0 33
∴ 2x = 3 or x = − 2 Find the solutions by putting each factor equal to zero
∴ x = -3/2 or x = −2 (4) - 2x2 = 32
2x2 – 32 = 0 Write in standard form with all the terms on one side and equal to 0
x2 – 16 = 0 Divide every term on both sides by 2
(x + 4)(x – 4) = 0 3 Factorise (the difference of two squares)
∴ x + 4 = 0 or x – 4 = 0
∴ x = –4 or ∴ x = 4 (4) - 3x + 1/x = 4, x ≠ 0 Multiply through by x to get rid of the denominator
3x2 + 1 = 4x Write in standard form with all the terms on one side and equal to 0
3x2 – 4x + 1 = 0 Factorise (the trinomial)
(3x – 1)(x – 1) = 0
∴ 3x – 1 = 0 or x – 1 = 0
∴ 3x = 1 or x = 1
∴ x = 1/3 or ∴ x = 1 (5) - 2 √x − 3 = x − 3 Square both sides
(2 √x − 3)2 = (x − 3)2
4(x − 3 ) = ( x − 3 ) ( x − 3 )
4x − 12 = x2 − 6x + 9
0 = x2 − 10x + 21
0 = ( x − 7 ) ( x − 3 )
∴ x − 7 = 0 or x − 3 = 0
∴ x = 7 or x = 3 (5)
[22]
|
Check your answers:
x = 7
LHS = 2 √7 − 3 = 2 √4 = 2(2) = 4 RHS = 7 − 3 = 4 ∴ x = 7 is a solution
x = 3
LHS = 2 √3 − 3 = 2 √0 = 0 RHS = 3 − 3 = 0 ∴ x = 3 is a solution
If a quadratic equation cannot be factorised, there are other ways to find the roots or solutions. Sometimes the solutions do not exist!
Activity 3
- What term can be added to the following equations to make a complete square?
- 0 = x2 – 8x + ?
- y = x2 + 9x + ?
- y = x2 -b/a x + ?
- Solve for x by using the method of completing the square.
- –3x2 + 5x + 4 = 0
- ax2 + bx + c = 0 [17]

Activity 4: Interpret a graph
Solve for x (correct to two decimal places):
4x2 – 8x = 7
2x (3x + 5) – 11 = 0 [9]
Solutions
1. 4x2 – 8x = 7 Write the equation in standard form (ax2 + bx + c = 0)
4x2 – 8x = 7 = 0 List the values of a, b and c
a = 4; b = – 8; c = –7 Write down the formula
x = − b ± √b2 − 4ac Substitute the values for a, b and c into the formula.
2
x = – ( –8 ) ± √(–8 ) 2 – 4(4)(–7) Simplify the value under the square root sign
2(4)
x = 8 ± √176 Separate the positive and negative value of the square root
8
x = 8 + √176 or x = 8 – √176 Answers in surd form
8 8
x = 2,66 3 or x = –0,66 3 Answers correct to two decimal places (5)
2. 2x(3x + 5) – 11 = 0 Write the equation in standard form
6x2 + 10x – 11 = 0 (ax2 + bx + c = 0)
x = –10 ± √100 + 26
12
= –10 ± √364
12
= –5 ± √91
6 (4)
[9]
These roots are irrational. Unless the question asks for decimal values,
leave them in surd form (the square root form).
|
Activity 5
Solve for x if
- (x+3)(x – 5) ≤–12
- –x ≤ 2x2 – 3 [10]
Solutions- (x+3)(x – 5) ≤ –12
x 2 – 2x – 15 +12 ≤ 0 Get into the standard form (ax2 + bx + c ≤ 0)
x 2 – 2x –3 ≤ 0 3
Factorise the trinomial:
(x –3)(x + 1) ≤ 0 3
Critical values:
x = 3 and x –1
We now indicate 3 and –1 on a number line.
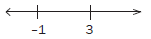
We know that the expression x2 – 2x –3 = 0 at x = 3 and x = –1. We can indicate this on the number line.
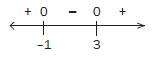
Our next step is to choose values less than –1, values between –1 and 3 and values greater than 3 and substitute it into the expression x 2 – 2x –3. If the answer is positive, then we indicate + on the number line. If the answer is negative, we indicate – on the number line
(If x = –10, then 2(–10)² +(–10) – 3 = 187 > 0 ∴ +
If x = 0, then 2(0)² – 0 –3 = –3 < 0 ∴ –
If x = 3, then 2(3)² + 3 – 3 = 18 > 0 ∴ +)
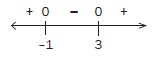
We have to solve for x where x2 – 2x –3 ≤ 0. The solution on the number line is the interval where we see zero and a negative. This happen when the x values are less than or equal to 3 and are also more than or equal to –1.
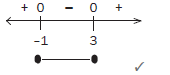
Therefore the solution is : − 1 ≤ × ≤ 3 (5) - –x ≤ 2x2 – 3
–2x2 – x + 3 ≤ 0 Get into the standard form (ax2 + bx + c ≤ 0)
–2x – x + 3 ≥ 0
-1 -1 -1 -1
Divide both sides by –1 to change the coefficient of x2 to a positive
2x2 + x – 3 ≥ 0 3 Factorise the trinomial
(2x + 3)(x – 1) ≥ 0 3
Critical values:
x = –3/2 and x = 1
We now indicate –3/2 and 1 on a number line.
We know that the expression 2x2 + x – 3 = 0 at x = –3/2 and x = 1.
We can indicate this on the number line.
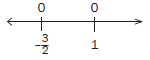
Our next step is to choose values less than –3/2, values between–3/2 and 1 and values greater than 1 and substitute it into the expression 2x2 + x – 3. If the answer is positive, then we indicate + on the number line. If the answer is negative, we indicate – on the number line
(Whenever we multiply or divide an inequality by a negative, the inequality sign changes i.e. the less or equal to sign changes to a greater or equal to sign.
If x = –10, then (–10)² 2(–10) – 3 =117 > 0 ∴ +
If x = 1, then (1)² – 2(1) – 3 =–4 < 0 ∴ –
If x = 5, then (5)² –2(5) – 3 = 12 > 0 ∴ +)
We have to solve for x where 2x2 + x – 3 ≥ 0. The solution on the number line is the interval where we see zero and a positive. This happens for the x values less than or equal to –3/2 and for the x values greater than or equal to 1.
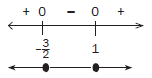
Therefore the solution is : x ≤ − –3/2 or x ≥ 1 33 (5)OR ALTERNATIVE METHOD by using a rough sketch of the parabola:
–x < 2x2 – 3 Get into the standard form ax2 + bx + c < 0
–2x2– x + 3 < 0 Divide both sides by –1.
–2x – x + 3 > 0 This is necessary to draw the rough sketch of a “positive” parabola
-1 -1 -1
2x2 + x – 3 > 0 3 With 0 on RHS
(2x + 3)(x – 1) > 0 3 Factorise LHS
Critical values of x: –3/2 and = 1 Make a rough sketch of a parabola
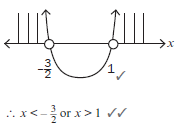
If (***)(***) > 0 (it means where y is positive)
Read off the x values of the graph above the x-axis (5)
[10]
|
Activity 6
Solve the following equations simultaneously.
1. 2x + y = 3 and x2 + y + x = y2
2. y = − 6 − 2 and y = − 3x + 2
x + 1
[14]
Solutions- 2x + y = 3 ………………… eqn (1)
x2 + y + x = y2 ………….. eqn (2)
y = –2x + 3 ………….. eqn (3) Use the linear equation (1) to write y alone on one side of the equation.
Substitute eqn (3) into eqn (2), to eliminate the y variable.
x2 + (–2x + 3) + x = (–2x + 3)2 3 Simplify both sides.
x2 – x + 3 = 4x2 – 12x + 9 Factorise the trinomial.
0 = 3x2 – 11x + 6
0 = (3x – 2)(x – 3)
∴ 3x – 2 = 0 or x – 3 = 0
∴ x = 2/3 or ∴ x = 3
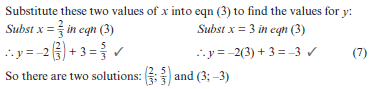 - y = − 6 − 2 and y = − 3x + 2
x + 1
y = − 6 − 2…………………(eqn 1)
x + 1
y = –3x + 2…………………..(eqn 2)
y is alone on one side of both equations.
∴ y = − 6 − 2 = –3x + 2 …………LCD = x + 1
x + 1
∴ –6 –2(x + 1) = –3x(x + 1) + 2(x + 1)
∴ –6 –2x –2 = –3x2 – 3x + 2x + 2
∴ 3x2 – x – 10 = 0
∴ (3x + 5)(x – 2) = 0
∴ x = -5/3 or x = 2
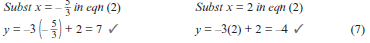
[14] |
Activity 7
- Show that the roots of x2 – 2x – 7 = 0, are irrational, without solving the equation. (3)
- Show that x2 + x + 1 = 0 has no real roots. (3)
- If x = 2 is a root of the equation 3x2 – 5x – 2k = 0, determine the value of k. (2)
- The solutions to a quadratic equation are: x = 5 ± √12 − 3a .
For which value(s) of a will the equation have equal roots. (3) - Determine the value(s) of k for which the equation 3x2 + (k + 2) x + k = 0 has equal roots (4)
[15]
Solutions- a = 1; b = –2 ; c = –7
Δ = b2 – 4ac = (–2)2 – 4(1)(–7)
= 4 + 28
= 32
∴ The roots will be irrational
(Δ > 0 and not a perfect square) (3) - a = 1; b = 1; c = 1
Δ = b2 – 4ac = (1)2 – 4 (1)(1)
= 1 – 4 = – 3
∴ There are no real roots
(Δ < 0 ) (3) - If 2 is a root of the equation, then x = 2. Therefore, we can substitute x = 2 into the equation.
3x2 – 5x – 2k = 0
∴ 3(2)2 – 5(2) –2k = 0
∴ 12 − 10 − 2k = 0
∴ 2k = 2
∴ k = 1 3 (2) - The equation will have equal roots if Δ = 0
Δ = 12 – 3a
0 3 = 12 − 3a
− 12 = − 3a
∴ a = 4 (3) - 3x2 + (k + 2)x + k = 0
∴ a = 3 ; b = (k + 2) ; c = k
∴ Δ = b2 – 4ac
= (k + 2)2 – 4(3)(k)
= k2 + 4k + 4 – 12k
= k2 – 8k + 4
For equal roots the Δ = 0
∴ k2 – 8k + 4 = 0
∴ k = 8± √(–8 ) 2 –4(1)(4)
2(1)
∴ k = 8± √48
2
∴ k = 7,46 or k = –0,54 (4)
[15]
|









