Probability Questions and Answers Mathematics Grade 12 Pdf Download. Probability is simply how likely something is to happen. Whenever we’re unsure about the outcome of an event, we can talk about the probabilities of certain outcomes—how likely they are. The analysis of events governed by probability is called statistics.
PROBABILITY QUESTIONS AND ANSWERS GRADE 12
Activity 1
- If S = {1; 2; 3; 4; 5; 6; 7}, A = {1; 3; 5; 7} and B = {2; 4; 6}, what is the probability of choosing a number that is not in set A? (2)
- S = {a; b; c; d; e; f; g; h; i; j} and A = {a; e; i}, B = {b; c; d; f; g; h}, C = {b; h; j}.
- Draw a Venn diagram to represent S. (4)
- Give a description of set A. (1)
- Are there any complementary sets? Explain. (2)
- Which sets are mutually exclusive, but they are not complementary? Give a reason for your answer. (2)
- A DVD shop has 180 comedies, 250 drama films, 230 science fiction movies and 120 thrillers. If you select a DVD at random, what is the probability that this movie is a comedy OR a thriller? (3)
[14]
- Complement: (noun) something that completes an event; it adds what is missing to make up the whole.
- Complementary: (adjective) an event that completes or adds to other events to make up the whole sample space.
NOTE: A complement is not the same as a compliment!
A compliment is a positive comment made to a person or a group of people.
Solutions- P(A´ ) = 1 – P(A) = 1 – 4/7 = 3/7 (2)
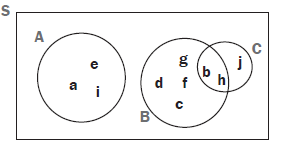 (4) (4)- Set A is the set of vowels from a to j; or the set of the first three vowels of the alphabet. (1)
- Sets A and B are not complementary because they do not include element j. Sets A and C are also not complementary.
Sets B and C share elements b and h, so they are not mutually exclusive or complementary. (2) - Set A and set B are mutually exclusive, but they are not complementary.
They do not share any elements, but they do not make up the whole sample space. Set A and Set C are also mutually exclusive, but not complementary. (2)
- No DVD is marked as both a comedy and a thriller, so there is no overlap in events. These are mutually exclusive (but not complementary).
There are 250 + 230 + 120 = 600 DVDs in the sample space.
Use P(A or B) = P(A) + P(B).
P(comedy or thriller) = P(comedy) + P(thriller)
= 180 + 120 = 300 = 5
780 780 780 13 (3)
[14]
|
Activity 2
In a group of 50 learners, 35 take Mathematics and 30 take History.
12 learners do not take Mathematics or History.
- Draw a Venn diagram to represent this information. (4)
- If a learner is chosen at random from this group, what is the probability that he takes both Mathematics and History? (2)
[6]
Solutions- Use M for Mathematics and H for History.
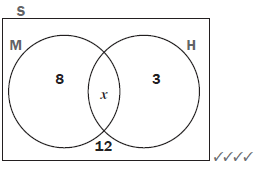 (4) (4)
- Draw the sample space and sets for the events M and H.
- We do not know yet how many learners (outcomes) are in the intersection of M and H.
So let M ∩ H = x - We do know that 12 learners are not in M or H.
35 – x + x + 30 – x + 12 = 50
–x = –27
x = 27
So place 27 in the intersection of M and H.
M = 35 – 27 = 8
H = 30 – 27 = 3.
- P(M and H) = 27/50 (2)
[6]
|
Activity 3
A school organised a camp for 103 Grade 12 learners. The learners were asked which food they prefer for the camp.
They had to choose from chicken (C), vegetables (V) and fish (F).
The following information was collected:
- 2 learners do not eat chicken, fish or vegetables
- 5 learners eat only vegetables
- 2 learners only eat chicken
- 21 learners do not eat fish
- 3 learners eat only fish
- 66 learners eat chicken and fish
- 75 learners eat vegetables and fish
Let the number of learners who eat chicken, vegetables and fish be x.
- Draw a Venn diagram to represent the information. (6)
- Calculate x. (3)
- Calculate the probability that a learner, chosen at random:
- Eats only chicken and fish, and no vegetables. (2)
- Eats any TWO of the given food choices: chicken, vegetables and fish. (2)
[13]
Solutions:-
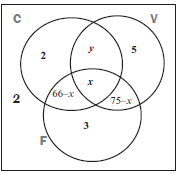
Fill in any given information that you can.
We do not know where these belong yet:
- 21 learners do not eat fish
- 66 learners eat chicken and fish
So let x be learners who eat chicken, fish and vegetables.
Then 66 – x is learners who eat only chicken and fish.
Introduce y, the learners who do not eat fish, but do eat chicken and vegetables.
Then 2 + y + 5 + 2 = 21
∴ y = 12 (6)
- 2 + 12 + 5 + 66 – x + x + 3 + 75 –x + 2 = 103
–x + 165 = 103
–x = –62
x = 62 (3) - 66 – x = 4 (2)
103 103 - 4+12+13 = 29
103 103 (2)
[13]
|
Activity 4
- P(A) = 0,45; P(B) = 0,3 and P(A or B) = 0,165.
Are the events A and B:- mutually exclusive
- independent (7)
- What is the probability of throwing at least one six in four rolls of a regular die? (3)
- What is the probability of throwing four 6s in a row with four rolls of a regular die? (3)
- If two dice are rolled at the same time, what is the probability that the sum of the two numbers is 9? (3)
[16]

Solutions- P(A or B) = P(A) + P (B) – P(A and B)
Events A and B are mutually exclusive if P(A and B) = 0
∴ if events are mutually exclusive, then P(A or B) = P(A) + P(B)
P(A or B) = 0,165
P(A) + P(B) = 0,45 + 0,3 = 0,75
∴ P(A or B) ≠ P(A) + P(B) (3)
Events A and B are not mutually exclusive. - Events A and B are independent if P(A and B) = P(A) × P(B)
To work out P(A and B), use the rule for P(A or B):
P(A or B) = P(A) + P(B) – P(A and B) for all events A and B
0,165 = 0,45 + 0,3 – P(A and B)
∴ P(A and B) = 0,75 – 0,165 = 0,585
But P(A) = 0,45 and P(B) = 0,3 ∴ P(A) × P(B) = 0,45 × 0,3 = 0,135
∴ P(A and B) ≠ P(A) × P(B)
∴ Events A and B are not independent. (4)
- The probability of not throwing a six in 4 rolls of a die is:
P(6) = (5/6)4 = 625
1296
∴ P(at least one 6) = 1 − 625 = 671
1296 1296 (3) - Each roll of the die is independent of the previous one.
P(four 6s in a row) = 1/6 x 1/6 x 1/6 x 1/6 = 1/1296 (3) - Use a table:
Let the columns represent die 1 and the rows represent die 2. | Die 1 | | Die 2 | | 1 | 2 | 3 | 4 | 5 | 6 | | 6 | 1;6 | 2;6 | 3;6 | 4;6 | 5;6 | 6;6 | | 5 | 1;5 | 2;5 | 3;5 | 4;5 | 5;5 | 6;5 | | 4 | 1;4 | 2;4 | 3;4 | 4;4 | 5;4 | 6;4 | | 3 | 1;3 | 2;3 | 3;3 | 4;3 | 5;3 | 6;3 | | 2 | 1;2 | 2;2 | 3;2 | 4;2 | 5;2 | 6;2 | | 1 | 1;1 | 2;1 | 3;1 | 4;1 | 5;1 | 6;1 |
There are 4 throws of both dice that give numbers with a sum of 9.
∴ P(sum of 9) = 4/36 = 1/9 (3)
[16]
|
Activity 5
- Determine the number of permutations that can be formed from all the letters of the word ABRACADABRA. (4)
- Determine the number of permutations that can be formed from all the letters of the word ABRACADABRA. This time, the first and last letters must be A. (4)
- Determine the number of permutations that can be formed from all the letters of the word ABRACADABRA. This time, all the As have to be next to each other. (4)
[12]
Solutions- There are 11 letters (so n = 11), but some letters are repeated.
There are 5 As; 2 Bs; 2 Rs; 1 C and 1 D.
The number of permutations will be 11! = 83 160 (4)
5!2!2!1!1!
On a calculator, use the multiplication sign between factorial factors. - The first and last letters are ‘fixed’, so there are 9 letters that can change positions
(n = 9). There are 3 As; 2 Bs; 2 Rs; 1 C and 1 D.
The number of permutations will be 9! = 15 120 (4)
3!2!2!1!1! - Treat ‘AAAAA’ as one possible outcome, so we have n = 7.
There are one AAAAA; 2 Bs; 2 Rs; 1 C and 1 D.
The number of permutations will be 7! = 1 260 (4)
1!2!2!1!1!
[12]
|
Activity 6
- At Angelo’s pizza place you can choose from 6 different types of pasta and 28 different sauces. How many different meals of 1 type of pasta and 1 type of sauce can you have? (2)
- In how many different ways can we arrange 7 books on a shelf ? (2)
- In how many different ways can 9 girls sit on one side of a table? (2)
- In how many ways can a three-letter word be made from the letters c; d; e; f without repeating any letters? (3)
- How many possible choices can be made in a multiple choice quiz if there are 4 questions each with 3 answers? (3)
- How many different words can be made using the letters from LIMPOPO? (4)
- How many 3-digit numbers can be made with the digits 1 – 5 if:
- repetitions are allowed (2)
- repetitions are not allowed (3)
- A code is made using the format XYY, where the X is any letter in the alphabet and Y represents any digit from 0 to 9.
- How many possible codes can be formed if the letters and digits are repeated? (3)
- How many possible codes can be formed if the letters and digits are not repeated? (3)
[27]
Solutions- 6 × 28 = 168 different meals. (2)
- 7! = 5 040 different ways 7 books can be arranged on a shelf. (2)
- 9! = 362 880 different ways for 9 girls to sit on one side of a table. (2)
- 4P3 = 4! = 4! = 24 ways a 3-letter word can be made from c; d; e; f with no repetition. (3)
(4-3)! 1! - 4 ‘boxes’ of 3 ∴ 3 × 3 × 3 × 3 = 34 = 81 possible choices. (3)
- LIMPOPO m = 7; one L; one I; one M; two Ps; two Os.
7! = 1 260 (4)
1!×1!×1!×2!×2!- 5 ‘boxes’ of 3 = 53 = 125 3-digit numbers (repetitions allowed) (2)
- 5P3 = 5! = 5! = 60 3-digit numbers (no repetition allowed) (3)
(5-3)! 2!
- In first slot, we have 26 possible options (26 letters in the alphabet)
In the second slot, we have 10 possible options (digits 0 to 10)
In the third slot, we have 10 possible options (digits 0 to 10 – the digits may be repeated)
∴ 26 × 10 × 10 = 2 600 possible codes (3) - In first slot, we have 26 possible options (26 letters in the alphabet)
In the second slot, we have 10 possible options (digits 0 to 10)
In the third slot, we have 9 possible options (the digits may be repeated)
∴ 26 × 10 × 9 = 2 340 possible codes (3)
[27]
|


 (4)
(4) (4)
(4)