Euclidean Geometry Questions and Answers Mathematics Grade 12 Pdf Download

Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry, Elements. Euclid’s approach consists in assuming a small set of intuitively appealing axioms and deducing many other propositions from these. Euclidean Geometry Questions and Answers Mathematics Grade 12 Pdf Download

EUCLIDEAN GEOMETRY QUESTIONS AND ANSWERS GRADE 12

Activity 1

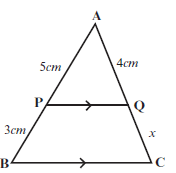
1. Determine the value of x, in the diagram alongside, if PQ ∣∣ BC. (4)
   

   Solution AP = AQ (PQ ∣∣ BC, prop theorem) PB    QC ∴ 5/3 = 4/x ∴ 5x = (3)(4) ∴ x = 12/5 = 2,4 cm 3 [4]

2. In ∆ABC, AB ∣∣ FD; AF ∣∣ DE and FE : EC = 3 : 4.
   Determine EC : BF (7)
   
   NOTE:
   3 : 4 does not mean that
   FE = 3 and EC = 4.
   For any a, we can say that
   FE = 3a and EC = 4a
   For every 3 of a in FE, there is
   4 of a in EC.

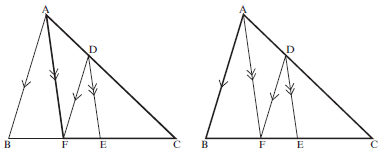
   Solution Work with two different triangles: ∆ACF and  ABC In ∆ACF: AD = FE (AF ∣∣ DE, prop intercept theorem) DC   EC In ∆ABC: AD = BF (AB ∣∣ FD, prop intercept theorem) DC    FC ∴ FE = BF(both = AD) EC   FC             DC FE = 3a and BF = BF EC    4a       FC     7a ∴ 3a = BF 4a    7a ∴ BF = 3(7a/4) = 21a____4 ∴ EC   = 4a ÷ 21a/4 BF = 4a ×  4 1    21a = 16 21 ∴ EC : BF = 16 : 21 [7]

3. Determine the value of x if PQ ∣∣ BC. (4)
   

   Solution AP = AQ (prop theorem , PQ ∣∣ BC) PB    QC 5/3 =  4/x 5x = (3) (4) x = 12/5 = 2,4cm [4]

4. In the diagram, RF ∣∣ KG , ED ∣∣ KH,
   RH = 3 units, RK = 9 units, HF = 2 units. GE: EK = 1:3
   
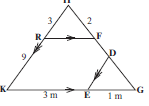
   Calculate (stating reasons) the lengths of:
   4.1 FG
   4.2 FD (8)

   Solutions 4.1 In ∆HKG FG = 9 S (line ∣∣ one side of a ∆) 3 R or (RF ∣∣ KG) 2     3 FG = 6 units S (3) 4.2 GD = GE = ¼ S (line ∣∣ one side of a ∆) 3 R or (ED ∣∣ KH) GH    GK GD =  ¼ .GH GD = ¼ .(8) S GD = 2 S ∴ FD = 6 − 2 = 4units 3 R OR In ∆HKG, HK ∣∣ DE GD = EG = 1/3 S DH    EK (line ∣∣ one side of a ∆) R or (proportional theorem, HK//DE ) 6 − FD = 1/3 S 2 + FD 18 − 3FD = 2 + FD ∴ FD = 4 units (5) [8]

Activity 2

1. Diameter AME of circle with centre M bisects FAB.
   MD is perpendicular to the chord AB.
   ED produced meets the circle at C, and CB is joined.
   
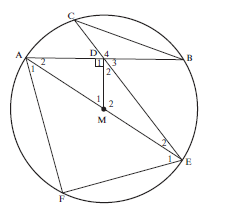
   1. Prove ∆AEF ||| ∆AMD (5)
   2. Hence, find the numerical value of AF. (5)
      AD
   3. Prove ∆ CDB ||| ∆ADE (4)
   4. Prove AD² = CD. DE (3)
      [17]

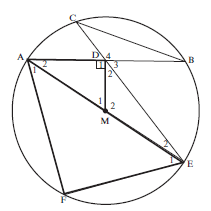
      Solution a) F = 90° (∠ in semi-circle) ^D1 = 90° (given MD ⊥ AB) ∴ ^F = ^D1 In ∆AEF and ∆AMD ^F = ^D1  (proved) ^A1 = ^A2 (AM bisects FAB) ∴ ^E1 = ^M1 (third ∠ of ∆) ∴ ∆AEF ∣∣∣ ∆AMD (AAA) or ∠∠∠ (5)	Solution b) AE = EF = AF (||| ∆s) AM    MD   AD AM = ME (radii) ∴ AE = 2AM ∴ 2AM = AF AM     AD ∴ AF = 2 (5) AD
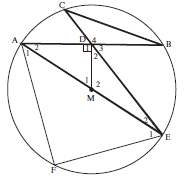
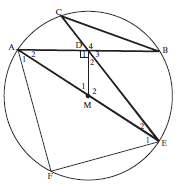
      c) In ∆CDB and ∆ADE ^C = ^A2 (∠s in same seg) ^B = ^E2 (∠s in same seg) ^D4 = ^D1 + ^D2 (opp ∠) ∴ ∆CDB ||| ∆ADE (AAA) (4)	Solution d) CD = DB  (III ∆s) AD     DE ∴ CD.DE = AD.DB But AD = DB (MD ⊥ AB, M is centre) ∴ CD. DE = AD ∴ AD2 = CD.DE (3) [17]

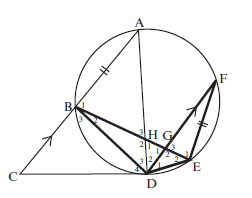
2. CD is a tangent to circle ABDEF at D.
   Chord AB is produced to C. Chord BE cuts chord AD in H and chord FD in G. AC ∣∣ FD and FE = AB
   
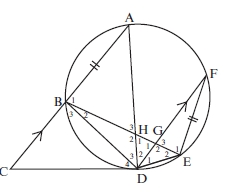
   1. Prove that ^D₄ = ^D₂ (3)
   2. Prove that ∆BHD ||| ∆FED (5)
   3. Hence AB = FD (3)
      BH    BD

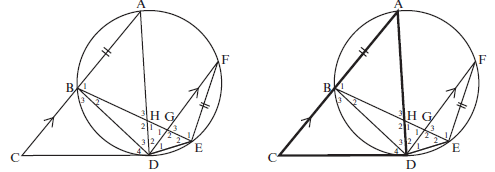
      Solutions a) ^A = ^D4 (tan-chord thm) ^D2 = ^A (alt ∠s CA ∣∣ DF) ^D4 = ^D2 (3) b) In ∆BHD and ∆FED ^B2 = ^F(∠s in same seg) ^D3 = ^D1 (equal chords) ^H2 = ^E2 (third ∠ of Δ) ∴ ∆BHD ||| ∆FED ∠∠∠ (5) c) FE = FD (||| ∆s) BH    BD But FE = AB (given) ∴ AB = FD (3) BH    BD [11]

      [11]

3. In the diagram ∆ABC is such that F is on AB and G is on AC. CB is produced to meet GF produced at E .DGFE is a straight line. BFA ∣∣ CD.
   AB = 20, BC = 10, EF = 8, EB = 5 and FB = 6.
   
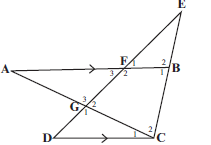
   3.1 Determine the numerical value of EF (3)
   ED
   3.2 Calculate the length of ED (2)
   3.3 Complete, without stating the reasons: ∆EFB III ∆ …. (1)
   3.4 Hence, calculate the length of DC (3)
   3.5 Prove that: AF = FG(4)
   CD    DG
   [13]

   Solutions BFA ∣∣ CD. AB = 20, BC = 10, EF = 8, EB = 5 and FB = 6 3.1 FB ll CD (Given) EF = EB S (line ∣∣ one side of A) 3 R ED    EC EF = 5 = 1 S (3) ED   15   3 3.2 EF = 1 from 3.1 and EF = 8 ED   3 ∴ 8  = 1 ED   3 ED = 24 S (2) 3.3 ∆EFB ∣∣∣ ∆EDC (1) 3.4 DC = ED (∆EFB ∣∣∣ ∆EDC) R FB     EF DC = 24 S 6       8 DC = 18 S (3) 3.5 In ∆AFG and ∆CDG ^A = ^C1 (alt ∠s. AF ∣∣ DC) S/R ^G3 = ^G1 (vertically opp ∠s) S/R ^F = ^D (alt ∠s. AF ∣∣ DC) ∆ AFG III ∆CDG (∠∠∠) R AF = FG (∆AFG ∣∣∣ ∆CDG) 3 R (4) CD    DG [13]

4. In the diagram, PQCB is a cyclic quadrilateral. Chords BP and CQ are produced to meet at A such that AQ = BC.
   
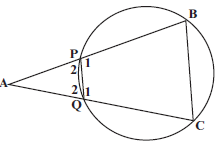
   4.1 Prove that: ΔAPQ III ΔACB (4)
   4.2 Hence, prove that AQ² = AB.PQ (3)
   [7]

   Solutions 4.1 Proof: In ΔAPQ and ΔACB ^A = ^A (common) S/R ^P2 = ^C S (ext ∠ of a cyclic quad ) 3 R ^P2 = ^ B (sum ∠s of ∆) or ( ext ∠ of cyclic quad ) ∆APQ ∣∣∣ ∆ACB ( ∠.∠.∠) R (4) 4.2 AQ = PQ S (∆APQ ∣∣∣ ∆ACB) S AB    BC AQ = PQ S ( AQ = BC ) AB     AQ AQ2 = AB.PQ (3) [7]